Lernpfad Islam
Vorbemerkung für die Unterrichtenden
In einigen Bundesländern soll der Islam schon recht früh in der weiterführenden Schule im christlichen Religionsunterricht vorkommen, manchmal sogar schon in der Grundschule. Das hat ja auch Sinn, denn viele Klassen aller Schulstufen sind aus Schülerinnen und Schülern mehrerer Konfessionen und Religionen zusammengsetzt. Dieser Lernpfad ist für Schülerinnen und Schüler der Stufe 5-7 konzipiert. Für die anderen Stufen muss im einzelnen entschieden werden, was verwendbar ist.
Mohammeds Biografie und die fünf Säulen des Islam
Ein erster Überblick
Nun hast Du schon einen ersten Einblick, welche Verpflichtungen Deine muslimischen Mitschülerinnen und Mitschüler mit ihrer Religion übernommen haben.
Wie es dazu gekommen ist, werden wir in den folgenden Abschnitten erfahren. Ein Problem dabei ist, dass die meisten Muslime Bilder ablehnen, andere lehnen Bilder dann ab, wenn es sich um Götzenbilder handelt. Daher gibt es Bilder von Muslimen, die Mohammeds Werdegang illustrieren. Im folgenden werden die Buchmalereien von Nakkas Osman aus dem 16. Jahrhundert verwendet.
Mohammeds Herkunft, Geburt und Jugend
Die Wissenschaftler nehmen an, dass Mohammed 570 n. Chr. in der arabischen Oasenstadt Mekka geboren wurde.
Mohammeds vollständiger Geburtsname lautet:
Abū l-Qāsim Muhammad ibn ʿAbdallāh ibn ʿAbd al-Muttalib ibn Hāschim ibn ʿAbd Manāf al-Quraschī
Aus seinem Namen geht hervor, dass er zur vornehmen arabischen Kaufmannsfamilie der Quraisch gehörte. Trotzdem verlief seine Kindheit nicht sehr glücklich: Sein Vater verstarb schon vor seiner Geburt; seine Mutter starb, als er sechs Jahre alt war. Danach nahm ihn sein Großvater auf, der aber zwei Jahre später ebfalls verstarb. Schließlich kam er zu seinem Onkel Abu Talib. Der junge Mohammed wollte offenbar möglichst früh auf eigenen Füßen stehen und arbeitete zuerst als Hirte, dann in einem der Handelshäuser von Mekka. Man kann sich gut vorstellen, wie er mit den Kamelkarawanen seines Arbeitgebers in fremde Städte gereist ist, um Handel zu treiben. Dabei lernte er viele unbekannte Dinge kennen, jüdische und christliche Gemeinden.
Er muss sehr tüchtig gewesen sein, denn als sein Arbeitgeber gestorben war, bot ihm dessen Witwe Chadidscha die Heirat an, so dass er mit 25 Jahren Eigentümer des Handelshauses wurde, in dem er fünf Jahre gearbeitet hatte.
Die Offenbarungen und die Predigt in Mekka
Mohammed begegnet dem Erzengel Gabriel
Im Alter von 40 Jahren war Mohammed ein gemachter Mann, wie man so sagt.
Doch er war offenbar nicht zufrieden, sondern zog sich immer wieder in die Berge in der Nähe seiner Heimatstadt Mekka zurück. Da spricht ihn während einer Meditation auf dem Berg Hira der Erzengel Gabriel an:
Im Namen des barmherzigen und gnädigen Gottes:
Predige im Namen deines Herrn, der den Menschen aus einem Embryo erzeugt hat. Predige die Worte der Schrift. Dein sehr edelmütiger Herr ist es, der den Menschen im Gebrauch des Schreibrohrs unterwiesen hat und ihm Dinge offenbart hat, die er zuvor nicht wusste.
(Sure 96, Verse 1-5)
Von da an suchte Mohammed, seine Landsleute davon zu überzeugen, dass es nur einen Gott gibt und dass die Verehrung der vielen Götzen, die in Mekka, vor allem am Zentralheiligtum, der Ka'aba, praktiziert wurde, den Menschen ins Verderben führt. Dieses zentrale Anliegen des Islam bringt die erste und wichtigste Verpflichtung des Muslim zum Ausdruck, das Bekenntnis
Die erste Säule des Islam: Das Glaubensbekenntnis (Schahada)
Das Bekenntnis lautet:
Ich bekenne:
Es ist kein Gott außer Gott.
Mohammed ist der Prophet.
Das Bekenntnis muss in arabischer Sprache ausgesprochen werden. In dem Film, der oben vorgeschlagen ist, um sich einen Überblick zu verschaffen, kann man sich das anhören und anschauen.
Die Kalligrafie (Schmuckschrift) des Glaubensbekenntnisses wird von Muslimen vielfach verwendet, z.B. als Amulett oder Schlüsselanhänger. Das Bild oben zeigt die Schahada als Schmuck an einer Moschee in Lahore (Pakistan).
Mohammed predigt den einen Gott - doch man glaubt ihm nicht.
Ibn Ishaq war im achten Jahrhundert der erste, der das Leben Mohammeds in geordneter Form beschrieben hat. Er erzählt: In einer Nacht brachte der Erzengel Gabriel dem Propheten das geflügelte Pferd Buraq. Auf diesem ritt er nach Jerusalem. Auf dem Tempelberg stieß sich Buraq mit gewaltiger Kraft ab und ritt mit Mohammed in den Himmel, damit er sehen konnte, wie die frommen Menschen von Gott belohnt werden. Danach ritt Mohammed in die Hölle und erlebte, welche Qualen den Ungläubigen bestimmt sind.
Der Fußabdruck des geflügelten Pferdes Buraq hat sich in den Felsen auf dem Tempelberg tief eingegraben und ist heute noch zu sehen. Über dem Felsen wurde der Felsendom zu Jerusalem errichtet, die drittheiligste Stätte des Islam.
Mohammed beschwor seine Landsleute, den Glauben an den einen Gott anzunehmen. Er gewann auch eine stattliche Zahl von Anhängern. Doch die Mächtigen in Mekka wollten den Glauben nicht annehmen. Sie befürchteten, dass niemand mehr zur Ka'aba pilgern würde, wenn nur noch ein Gott verehrt werden dürfte; niemand würde mehr Talismane und Amulette kaufen, und das gefährdete ihre Geschäfte.
Mohammeds Flucht und der Aufbau der ersten Moschee
Die Flucht Mohammeds von Mekka nach Medina (Hedschra)
Etwa im Jahre 619 starben Mohammeds wichtigste Unterstützer: Seine Frau Chadischa und sein Onkel Abu Talib. Seine Gegner gewannen in Mekka die Oberhand, und es wurden sogar Pläne geschmiedet, Mohammed aus dem Weg zu räumen. Der Prophet versteckte sich zuerst und brach dann auf, um in die 450 KM entfernte Stadt Jathrib überzusiedeln. Am 24. September 622 kam er in der Stadt an, die seither den Ehrennamen Medina - Stadt des Propheten - trägt. Damit beginnt die islamische Zeitrechnung.
Beginn der muslimischen Zeitrechnung
Wenn mit dem 24. September 622 die islamische Zeitrechnung beginnt, in welchem Jahr leben die Muslime heute? Die einfache Antwort 2020-622 ist gleich 1398 stimmt leider nicht, weil das islamische Jahr ein Mondjahr ist und nur 354 anstatt 365 Tage hat. (Schaltjahre, die es in beiden Kalenderrechnungen gibt, lassen wir der Einfachheit halber weg.)
Also müssen wir ausrechnen, wieviel islamische Jahre seit 622 vergangen sind, das sind 1398/354*365, also 1441 Mondjahre.
Das islamische Jahr 1441 hat am 1. September 2019 begonnen und wird am 20. August 2020 enden.
Der Unterschied zwischen unserem Sonnenkalender und dem islamischen Mondkalender bewirkt auch, dass der Fastenmonat Ramadan aus christlicher Sicht jedes Jahr 11 Tage früher anfängt und endet als im Vorjahr.
Aufbau der Moschee in Medina
Dieser Stahlstich aus dem 19. Jahrhundert zeigt die Prophetenmoschee in Medina noch in einem relativ bescheidenen Ausmaß. Die Wahhabiten haben an dieser Stelle eine gewaltige, zwei Millionen Menschen fassende, Moschee errichtet. Mohammed begann an dieser Stelle mit ein paar Holzhütten in einem Palmenhain, um dort mit seinen Anhängern erstmalig den Islam zu leben. Die Moschee (arab. Ort der Niederwerfung) wurde von den ersten Muslimen als Wohn- und Gebetsstätte und als Schule genutzt.
Die Zweite Säule des Islam: Das Beten (Salat)
Schau Dir den Anfängerkurs Pflichgebet (Video 5 MIN) an.
Du kennst das verbreitetste Gebet der Christen: Das Vater Unser. Vergleiche das christliche Beten mit dem muslimischen Gebet, wie Du es im Film erlebt hast.
Die dritte Säule des Islam: Die Almosensteuer (Zakat)
Zakat bedeutet Läuterung. Mohammed wollte mit dieser Verpflichtung also nicht nur für einen Ausgleich der Vermögensunterschiede unter Muslimen sorgen, sondern er wollte auch, dass sich die Gläubigen von Gier und Geiz reinigen.
Schlag nach in der deutschen Quran-Übersetzung die Sure 9, und suche dort den Vers 60. Schreib in einer Liste auf, für wen die Almosensteuer verwendet werden soll.
In der Pressemitteilung Trends und Prognosen 2018 des deutschen Spendenrats kannst Du Dich über das Spendenverhalten der deutschen Bevölkerung im Jahr 2018 informieren.
Benenne Spendenziele, die bei der Almosensteuer vorkommen, im Bericht des Spendenrates aber keine Rolle spielen.
Benenne auch Spendenziele, die offenbar für Deutsche heute wichtig sind, und die im Quran, Sure 9 Vers 60 nicht vorkommen.
Die vierte Säule des Islam: Der Fastenmonat (Ramadan)
Meine Freundinnen fragen immer, wie ich das schaffe mit dem Fasten und ob ich dazu gezwungen werde. Also, eigentlich müsste ich noch gar nicht fasten, weil ich noch nicht meine Tage habe. Aber ich will das mit meiner Familie mitmachen. Meine Mutter hat mir das Fasten so erklärt: Die anderen Verpflichtungen wie Beten und die Wallfahrt, das können ja alle sehen, ob ich da mitmache. Also kann ich damit auch angeben. Aber dass man nichts isst, dass man Hunger hat, das kann ja kein anderer sehen. Das mache ich also nur für Allah. Also freut sich Allah besonders über das Fasten, weil wir das nur für ihn machen und nicht für das Angeben.
Nachts dürfen wir etwas essen. Wenn der Ramadan in den Sommer fällt, müssen wir natürlich sehr früh aufstehen, damit wir vor dem Sonnenaufgang fertig sind mit dem Frühstücken. Aber Abends nach Sonnenuntergang ist es schön. Dann treffen wir uns in der muslimischen Jugendgruppe in der Moschee; alle essen zusammen, keiner wird ausgeschlossen. Meine Freundin Anna, die keine Muslima ist, war auch schon mal mit. Anna ist überhaupt sehr nett. Wenn ich faste, isst sie in der Schule auch nichts, um mich nicht neidisch zu machen.
Fasse kurz zusammen, was Fatima erzählt. Was, glaubst du, sind Fatimas Gründe, beim Fasten mitzumachen?
Mohammeds Wallfahrt nach Mekka und sein Tod
Mohammeds Wallfahrt nach Mekka und die Reinigung der Ka'aba"
Die Mekkaner ließen Mohammed und seine Anhänger nicht in Ruhe. Zwischen 624 und 628 kam es zu einer Reihe von verlustreichen Schlachten mit wechselndem Ausgang. Da beschloss Mohammed, zu einer Wallfahrt nach Mekka aufzubrechen, obwohl seine Gegner in der Stadt die Vorherrschaft besaßen und nach wie vor beabsichtigten, ihn zu töten.
Mohammed gelangte mit einigen Schwierigkeiten in die Stadt und umrundete das alte Heiligtum, die Ka'aba, den würfelförmigen Stein, der einst von Abraham und seinem Sohn Ismael aufgerichtet worden sein soll. Nun bekehrten sich führende Mekkaner zum Islam, Mohammed ließ die Götzenbilder aus dem Heiligtum entfernen, so dass die Ka'aba zum Haus Allahs wurde.
Die fünfte Säule des Islam: Die Hadsch
Im Gedenken an Mohammeds Wallfahrt nach Mekka sind jeder Muslim und jede Muslima gehalten, einmal in ihrem Leben nach Mekka zu reisen.
Mohammeds Tod in Medina
632 begibt sich Mohammed noch einmal auf Pilgerfahrt nach Mekka und legt bei dieser Wallfahrt genau fest, wie die Hadsch zu verrichten ist. In seiner Abschiedspredigt auf dem Berg Arafat sagt er:
Heute habe ich euch eure Religion vervollständigt, so dass nichts mehr daran fehlt, und meine Gnade an euch vollendet, und ich bin damit zufrieden, dass ihr den Islam als Religion habt. (Sure 9 Vers 3)
Am 8. Juni 632 (nach christlicher Zeitrechnung) ist Mohammed in Medina nach kurzer Krankheit verstorben. Manche wollen nicht glauben, dass der Prophet sterben muss, andere meinen, dass damit die Sache des Islam zuende ist. Doch Abu Bakr, der in der letzten Zeit schon Mohammed im Gebet vertreten hat, sagt:
Ihr Menschen, wenn jemand Mohammed anbetet: Mohammed ist tot.
Wenn jemand Gott anbetet, Gott lebt und wird nie sterben.
Die rechtgeleiteten Kalifen und die Zusammenstellung des heiligen Quran
Mit dem Tod Mohammeds beginnt die Zeit der rechtgeleiteten Kalifen (632-661) Kalif bedeutet auf Arabisch Stellvertreter.
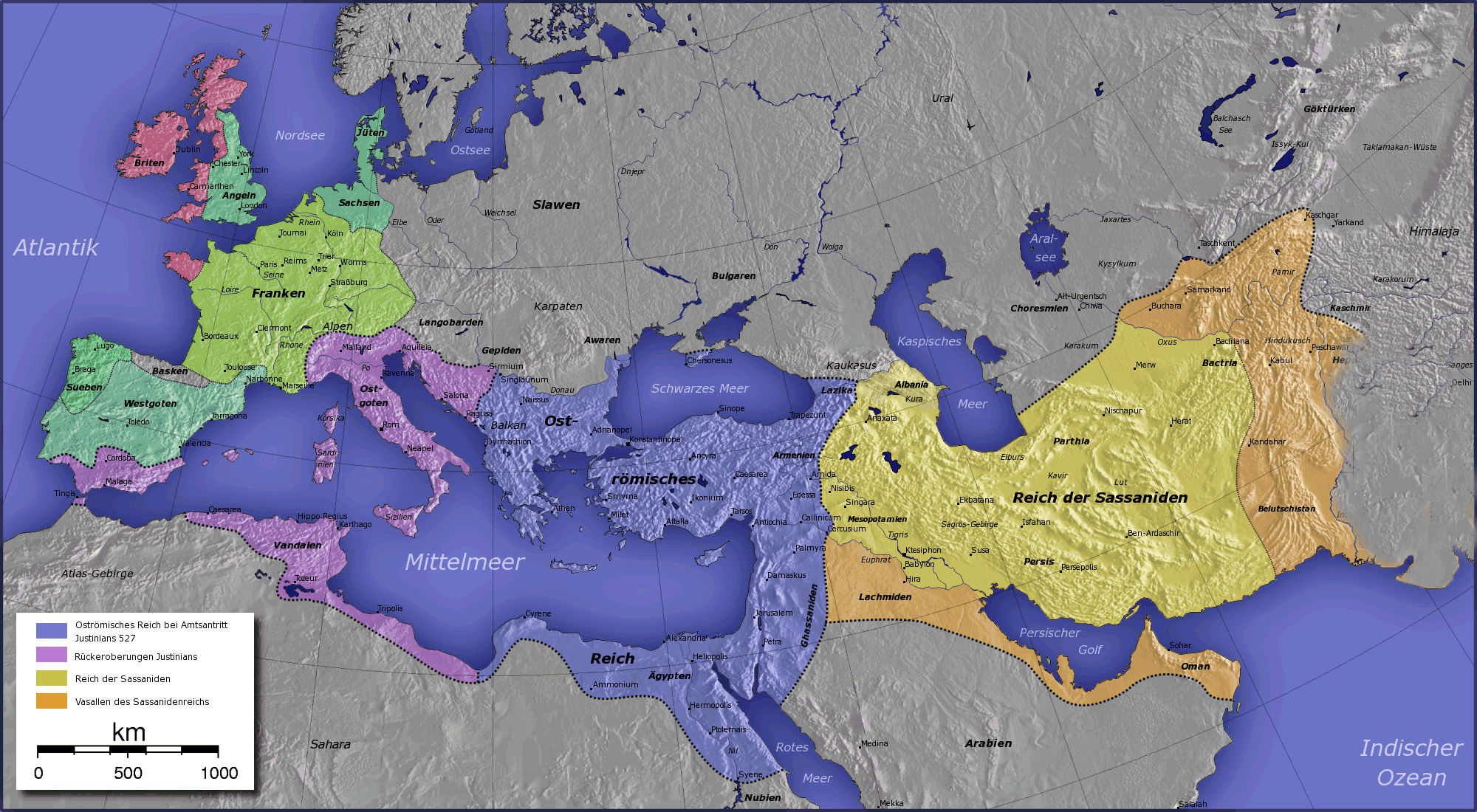
Welche Expansion der Islam in der Zeit Mohammeds und im Jahrhundert danach erreichte, kann der Vergleich zweier Karten illustrieren
Kaiser Justinian, der 527-565 herrschte, also unmittelbar vor der Geburt Mohammeds 570, konnte für das christliche oströmische Reich große Teile der Mittelmeerküste und die angrenzenden Gebiete zurückerobern. Die arabische Halbinsel war in Stammesgebiete aufgeteilt.
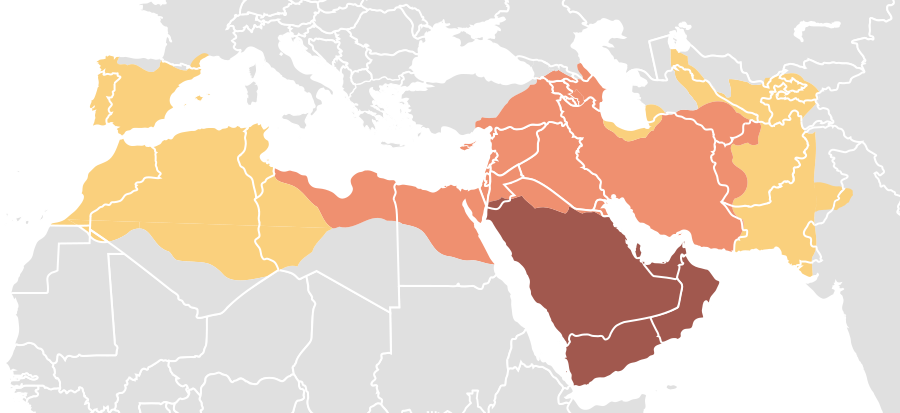
Ein Jahrhundert später sieht die Landkarte des östlichen Mittelmeerraums völlig anders aus:
Bereits zu Lebzeiten Mohammeds vereinten sich die Stämme Arabiens zu einem großen Volk mit einer einheitlichen Religion. (In der Karte braun markiert)
Die ersten Nachfolger Mohammeds erweiterten die muslimische Herrschaft nach Nordosten bis an die Grenzen Indiens und nach Westen bis nach Nordafrika (orange gefärbt), und unter dem Herrschergeschlecht der Umayyaden gingen die Eroberungen in alle Richtungen weiter.
Uthman, Mohammeds Schwiegersohn und der dritte seiner Nachfolger, ließ den heiligen Quran, die Sammlung der von Mohammed empfangenen Offenbarungen, in die Form bringen, die bis heute überliefert ist.
Neben den Hadithe, den Überlieferungen von Mohammed, und der Scharia, der lebendigen aktualisierenden islamischen Rechtsfindung, ist der Quran die wichtigste Richtschnur muslimischen Lebens und in muslimischen Ländern auch geltendes Recht.
Dabei haben sich unterschiedliche Auslegungstraditionen und Schulen gebildet, die früher in unterschiedlichen Gebieten nebeneinander existierten, im Zuge der Kolonialisierung und Globalisierung einander allerdings nahe gekommen sind - mit meistens, aber nicht immer friedlichen Folgen.